２つの正弦波の位相差を求める方法-03

ベクトル積と面積との関係

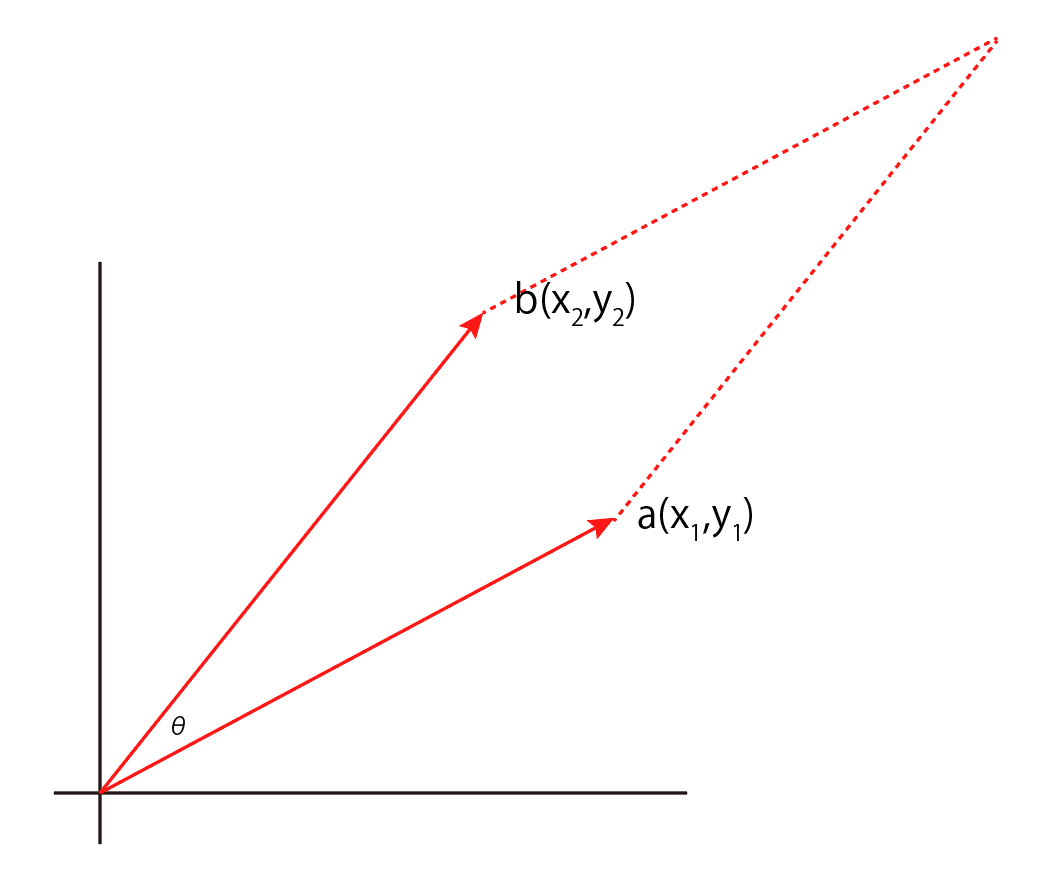
XYプロットにおいて，それぞれの座標と原点を結ぶベクトルを考えます．

このベクトルが刻一刻と楕円運動していくわけです．

そこで，２つのベクトルを考えていきます．それぞれ，

\(\Large a(x_1, y_1), \ b(x_2,y_2) \)　

とします．

その間のなす角を，θ，とします．

それぞれのベクトルの大きさは，

\(\Large a^2 = x_1^2 + y_1^2, \ b^2 = x_2^2 + y_2^2 \)　

です．この平行四辺形の面積，S，は，

\(\Large S = a \cdot b \cdot cos \ \theta \)　

\(\Large S^2 = a^2 \cdot b^2 \cdot cos^2 \ \theta \)　

\(\Large = a^2 \cdot b^2 \cdot ( 1 - cos^2 \theta) \)　

\(\Large = a^2 \cdot b^2 - a^2 \cdot b^2 \cdot cos^2 \theta \)　

となります．右辺第二項は内積となるので

\(\Large a \cdot b \cdot cos \theta = x_1 \cdot x_2 + y_1 \cdot y_2\)　

\(\Large S^2 = (x_1^2 + y_1^2)(x_2^2 + y_2^2) - (x_1 \cdot x_2 + y_1 \cdot y_2)^2 \)　

\(\Large = x_1^2 \cdot x_2^2 + x_1^2 \cdot y_2^2 + y_1^2 \cdot x_2^2 + y_1^2 \cdot y_2^2 - (x_1^2 \cdot x_2^2 +2 x_1 \cdot x_2 \cdot y_1 \cdot y_2 + y_1^2 \cdot y_2^2 ) \)　

\(\Large = x_1^2 \cdot y_2^2 - 2 x_1 \cdot x_2 \cdot y_1 \cdot y_2 + y_1^2 \cdot x_2^2 \)　

\(\Large = (x_1 \cdot y_2 - y_1 \cdot x_2)^2 \)　

\(\Large S = x_1 \cdot y_2 - x_2 \cdot y_1 \)　

となります．

別の方法として，面積から考えると，

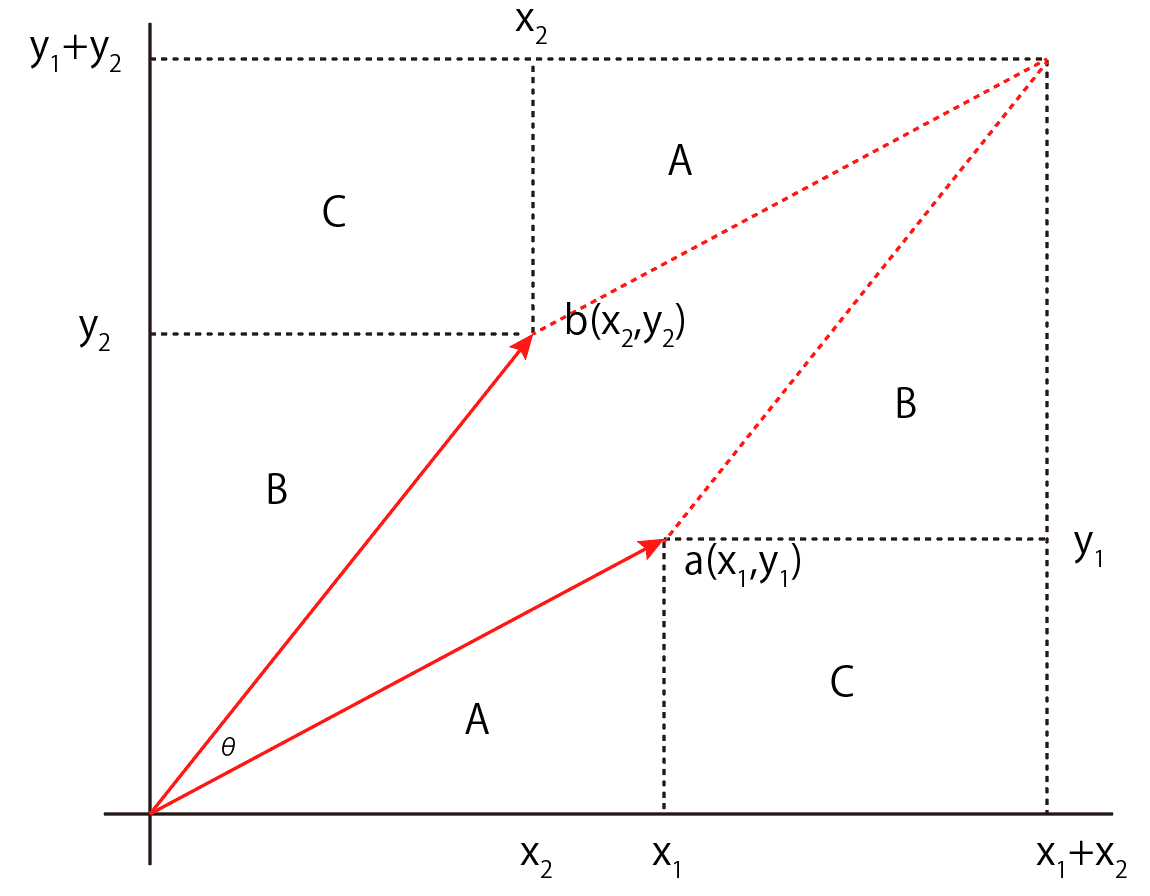
\(\Large S_{sqare} = (x_1 + x_2) \cdot (y_1 + y_2) \)　

\(\Large 2 \ S_A = x_1 \cdot y_1 \)　

\(\Large 2 \ S_B = x_2 \cdot y_2 \)　

\(\Large 2 C = 2 \ x_2 \cdot y_1 \)　

\(\Large S_{parallelogram} = (x_1 + x_2) \cdot (y_1 + y_2) - [ x_1 \cdot y_1 + x_2 \cdot y_2 + x_2 \cdot y_1 ] \)　

\(\Large = x_1 \cdot y_1 + x_1 \cdot y_2 + x_2 \cdot y_1 + x_2 \cdot y_2- [ x_1 \cdot y_1 + x_2 \cdot y_2 + x_2 \cdot y_1 ] \)　

\(\Large = x_1 \cdot y_2 - x_2 \cdot y_1 \)　

と ２つの導出結果が一致しました．

次ページから，この関係を用いて，ベクトル積と位相，との関係を考えていきます．